原文<BinarySpace Partioning Trees and Polygon Removal in Real Time 3D Rendering>

第一章 介绍

背景

二叉空间分割（BSP）树在1969年由Shumacher首次提出，当时并未想到能成为开发娱乐产品的算法，但从90年代初BSP树就已经被用于游戏行业来改善性能，并使利用地图中更多细节成为可能。第一个使用该技术的游戏是Doom，由游戏行业中的两位传奇人物JohnCarmack和John Romero创立。从那时起几乎所有的FPS游戏都使用了该技术。

 

问题陈述

由于游戏行业的激烈竞争，人们为了改善该算法的原始设计做了大量工作，我们相信改善是可能的。我们的主要焦点已经集中于将费时的运算从运行时移到预处理时，因此要建立一个运行时使用的能容纳大量信息的结构。另外我们希望利用BSP树的优点找到改善和优化游戏引擎中包围区域的方法。这份报告的“负作用”是可以作为如何开发游戏引擎的指南。

 

这份报告将指出：

l        什么是BSP树

l        如何创建BSP树

l        优点/缺点

l        可用的相似技术

l        BSP树的适用性

l        我们的方法与现有方法的比较

 

此理论的研究由瑞典游戏开发商O3games公司完成。研究结果用于姊妹公司CloopSystem发布的产品中。我们已经实现了全自动工作的BSP树，它拥有所有附属效应，在人们可以利用BSP树优点的领域。为了便于讨论，我们将从所写代码中提取示例。为了揭示已经完成的优化，当分析算法复杂度时，我们将使用类似C++的伪代码。大多数示例是在2D下说明，但它们在3D下也同样可以工作。整个报告中作者假定读者拥有3D数学和向量代数基本概念知识。

第二章 BSP Trees

如名字一样，BSP树是一个结构，将空间分割成为更小的子集，今天，随着硬件加速Z缓冲的出现，使对于空间给定位置能拥有更小数据量。但在90年代初使用BSP树的原因是它能将场景中多边形排序，然后从后到前画，意味着拥有最低Z值5的多边形将最后画。当然还有其他的算法可以完成这个功能，例如著名的画家算法，但是它与BSP比较起来速度太慢了，这是因为BSP通常对图元排序是预先计算好的而不是在运行时进行计算。从某种意义上说BSP技术实际上是画家算法的扩展，正如同BSP技术的原始设计一样，画家算法也是使用由后至前的顺序对场景中的物体进行渲染。但是画家算法有以下的缺点：

l 如果一个多边形从另一个多边形穿过时它不能正确渲染；

l计算每一帧要画的多边形顺序困难和昂贵；

l 算法不能处理如下图所示的循环重叠的情况。

            图1.1

BSP算法

创建BSP Trees的最初想法是获得一个场景中的多边形集合，然后分割这个集合为更小的子集，每个子集都是“多边形凸集”。这意味着子集中每一个多边形都在其它多边形的“前面”。是不是有点难以理解呢，举一个例子，如果多边形A的每一个顶点都位于由多边形B所组成的一个面的正面，那么可以说多边形A位于多边形B的“前面”，参考左图。我们可以想象一下，一个盒子是由6个面组成的，如果所有的面都朝向盒子的内部，那么我们可以说盒子是一个“凸多边形”，如果不是都朝向盒子的内部，那么盒子就不是“凸多边形”。                                                 

 图1.2

确定一个多边形集合是否是“凸集”的函数看起来像这样:

l CLASSIFY-POINT

l 入参:

l Polygon – 相对于点的多边形。

l Point – 相对于定义平面的3D点。

l 返回值:

l 点位于多边形的哪一边。

l 功能:

l 确定点位于多边形定义平面的哪一边。

CLASSIFY-POINT (Polygon, Point)

Sidevalue = Polygon.Normal * Point

if (Sidevalue == Polygon.Distance)

then return COINCIDING

else if (Sidevalue < Polygon.Distance)

then return BEHIND

else return INFRONT

l POLYGON-INFRONT

l 参数:

l Polygon1 – 用来确定其它多边形是否在其“前面”的多边形。

l Polygon2 – 检测是否在第一个多边形“前面”的多边形。

l 返回值:

l 第二个多边形是否在第一个多边形的“前面”。

l 功能:

l 检测第二个多边形的每一个顶点是否在第一个多边形的“前面”。

POLYGON-INFRONT (Polygon1, Polygon2)

1 for each point p in Polygon2

2 if (CLASSIFY-POINT (Polygon1, p) <> INFRONT)

3 then return false

4 return true

l 函数 IS-CONVEX-SET

l 参数:

l PolygonSet – 用来检测是否为“凸多边形”的图元集合。

l 返回值:

l 集合是否为“凸多边形”。

l 功能:

l 相对于集合中的其它多边形检查每一个多边形，看是否位于其它多边形的“前面”，如果有任意两个多边形不满足这个规则，那么这个集合不为“凸多边形”。

IS-CONVEX-SET (PolygonSet)

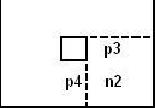
1 for i = 0 to PolygonSet.Length ()

2 for j = 0 to PolygonSet.Length ()

3 if(i != j && not POLYGON-INFRONT(PolygonSet[i], PolygonSet[j]))

4 then return false

5 return true

 

在函数POLYGON-INFRONT中并没有进行对称的比较，这意味着如果多边形A位于多边形B的“前面”你并不能想当然的认为多边形B一定位于多边形B的“前面”。下面的例子简单的显示了这一点。

       

                 图1.3

在图1.3中我们可以看到多边形1位于多边形2的“前面”，这是因为顶点p3、p4位于多边形2的“前面”，而多边形2却没有位于多边形1的“前面”，因为顶点p2位于多边形1的“后面”。

BSP树所需的结构可定义如下：

class BSPTree

{

BSPTreeNode  RootNode // 树的根节点

}

class BSPTreeNode

{

BSPTree Tree // 节点所属的树

BSPTreePolygon Divider // 位于两个子树之间的多边形

BSPTreeNode *RightChild // 节点的右子树

BSPTreeNode *LeftChild // 节点的左子树

BSPTreePolygon PolygonSet[] // 节点中的多边形集合

}

class BSPTreePolygon

{

3DVector Point1 // 多边形的顶点1

3DVector Point3 // 多边形的顶点2

3DVector Point3 // 多边形的顶点3

}

你将看到每个多边形只由3个点来表示，这是因为显卡硬件专为画三角形而设计。将多边形集合分割为更小的子集合有很多方法，例如你可以任意选择空间中的一个面然后用它来对空间中的多边形进行分割，把位于分割面正面的多边形保存到右子树中而位于反面的多边形保存到左子树中。使用这个方法的缺点非常明显，那就是如果想选择一个将空间中的多边形分割为两个相等的子集合的面非常困难，这是因为在场景中有无数个可选择的面。如何在集合中选择一个最佳的分割面呢？下面我将对这个问题给出一个比较适当的解决方案。

我们现在已经有了一个函数POLYGON-INFRONT，它的功能是确定一个多边形是否位于其它多边形的正面。现在我们要做的是修改这个函数，使它也能够确定一个多边形是否横跨过其它多边形定义的分割面。算法如下：

l 函数 CALCULATE-SIDE

l 参数 :

l Polygon1 – 确定其它多边形相对位置的多边形。

l Polygon2 – 确定相对位置的多边形。

l 返回值:

l 多边形2位于多边形1的哪一边

l 功能:

l 通过第一个多边形对第二个多边形上的每一个顶点进行检测。如果所有的顶点位于第二个多边形的正面，那么多边形2被认为位于多边形1的“前面”。如果第二个多边形的所有顶点都位于第一个多边形的反面，那么多边形2被认为位于多边形1的“后面”。如果第二个多边形的所有顶点位于第一个多边形之上，那么多边形2被认为位于多边形1的内部。最后一种可能是所有的顶点即位于正面有位于反面，那么多边形2被认为横跨过多边形1。

CALCULATE-SIDE (Polygon1, Polygon2)

 NumPositive = 0, NumNegative = 0

 for each point p in Polygon2

 if (CLASSIFY-POINT (Polygon1, p) = INFRONT)

 then NumPositive = NumPositive + 1

 if (CLASSIFY-POINT (Polygon1, p) = BEHIND)

 then NumNegative = NumNegative + 1

 if (NumPositive > 0 && NumNegative = 0)

 then return INFRONT

 else if(NumPositive = 0 && NumNegative > 0)

 then return BEHIND

 else if(NumPositive = 0 && NumNegative = 0)

 then return COINCIDING

 else return SPANNING

上面的算法也给我们解答了一个问题，当一个多边形横跨过分割面时如何进行处理，上面的算法中将多边形分割为两个多边形，这样就解决了画家算法中的两个问题：循环覆盖和多边形相交。下面的图形显示了多边形如何进行分割的。

             

图1.4

如图1.4所示，多边形1为分割面，而多边形2横跨过多边形1，如图右边所示，多边形被分割为2、3两部分，多边形2位于分割面的“前面”而多边形3位于分割面的“后面”。

当建立一个BSP树时，首先需要确定的问题是如何保证二叉树的平衡，这意味着对于每一个叶节点的分割深度而言不能有太大的差异，同时每一个节点的左、右子树需要限制分割的次数。这是因为每一次的分割都会产生新的多边形，如果在建立BSP树时产生太多的多边形的话，在图形加速卡对场景渲染时会加重渲染器的负担，从而降低帧速。同时一个不平衡的二叉树在进行遍历时会耗费许多无谓的时间。因此我们需要确定一个合理的分割次数以便于获得一个较为平衡的二叉树，同时可以减少新多边形的产生。下面的代码显示了如何通过循环多边形集合来获得最佳的分割多边形。

l 函数 CHOOSE-DIVIDING-POLYGON

l 参数:

l PolygonSet – 用于查找最佳分割面的多边形集合。

l 返回值:

l 最佳的分割多边形。

l 功能:

l 对指定的多边形集合进行搜索，返回将其分割为最佳子集合的多边形。如果指定的集合是一个“凸多边形”则返回。

CHOOSE-DIVIDING-POLYGON (PolygonSet)

1 if (IS-CONVEX-SET (PolygonSet))

2 then return NOPOLYGON

3 MinRelation = MINIMUMRELATION

4 BestPolygon = NOPOLYGON

5 LeastSplits = INFINITY

6 BestRelation = 0

l 循环查找集合的最佳分割面。

7 while(BestPolygon = NOPOLYGON)

8 for each 多边形P1 in PolygonSet

9 if (多边形P1在二叉树建立过程中没有作为分割面)

l 计算被当前多边形定义的分割面的正面、反面和横跨过分割面的多边形的数量。

10 NumPositive = 0, NumNegative = 0, NumSpanning = 0

11 for each 多边形P2 in PolygonSet except P1

12 value = CALCULATE-SIDE(P1, P2)

13 if(value = INFRONT)

14 NumPositive = NumPositive + 1

15 else if(value = BEHIND)

16 NumNegative = NumNegative + 1

17 else if(value = SPANNING)

18 NumSpanning = NumSpanning + 1

l 计算被当前多边形分割的两个子集合的多边形数量的比值。

19 if (NumPositive < NumNegative)

20 Relation = NumPositive / NumNegative

21 else

22 Relation = NumNegative / NumPositive

l 比较由当前多边形获得的结果。如果当前多边形分割了较少的多边形同时分割后的子集合比值可以接受的话，那么保存当前的多边形为新的候选分割面。

l 如果当前多边形和最佳分割面一样分割了相同数量的多边形而分割后的子集合比值更大的话，将当前多边形作为新的候选分割面。

23 if (Relation > MinRelation &&

(NumSpanning < LeastSplits ||

(NumSpanning = LeastSplits &&

Relation > BestRelation))

24 BestPolygon = P1

25 LeastSplits = NumSpanning

26 BestRelation = Relation

l 通过除以一个预先定义的常量来减少可接受的最小比值。

27 MinRelation = MinRelation / MINRELATIONSCALE

28 return BestPolygon

算法分析

对于上面的函数来说，根据场景数据大小的不同它可能花费很长一段时间。常量MINRELATIONSCALE用来确定在每次循环时所分割的子集合多边形数量的比值每次减少多少，为什么要使用这个常量呢，考虑一下，对于给定的MinRelation如果我们找不到最佳的分割面，通过除以这个常量将比值减少来重新进行循环查找，这样可以防止死循环的出现，因此当这个比值足够小时我们必定可以获得可接受的最佳结果。最坏的事情是我们有一个包含N个多边形的非“凸”集合，分割多边形将集合分割为一个包含N-1个多边形的部分和一个包含1个多边形的部分。这个结果只有在最小比值小于1/(n-1)才是可以接受的（参考算法的19-23行）。这意味着MinRelation /MINRELATIONSCALEi < 1/(n-1)，这里i是循环重复的次数。让我们假设MinRelation的初始化值为1，由于比值永远为0-1之间的值因此这是最可能的值（参考算法的19-22行）。我们有

1 / MINRELATIONSCALEi < 1/(n-1)

1 < MINRELATIONSCALEi/(n-1)

(n-1) < MINRELATIONSCALEi

logMINRELATIONSCALE (n-1) < i

这里的i没有上边界，但是因为i非常接近于logMINRELATIONSCALE (n-1)，我们可以简单的假设两者是相等的。另外我们也假设MINRELATIONSCALE永远大于或等于2，因此我们可以有

logMINRELATIONSCALE (n-1) = i 

MINRELATIONSCALE >= 2

i = logMINRELATIONSCALE (n-1) < lg(n-1) = O(lg n)

在循环的内部，对多边形的集合需要重复进行两次循环，因此对我们来说最坏的情况下这个算法的复杂度为O(n2lg n)，而通常情况下这个算法的复杂度接近于O(n2)。

在函数CHOOSE-DIVIDING-POLYGON的循环中看起来如果不发生什么事情的话好象永远不会停止，但是这不会发生，这是因为如果多边形集合为非“凸”集合的话总能找到一个多边形来把集合分割为两个子集合。CHOOSE-DIVIDING-POLYGON函数总是选择分割集合的多边形数量最少的多边形，为了防止选择并不分割集合的多边形，分割后的子集合的多边形数量之比必须大于预先定义的值。为了更好的理解我上面所讲解的内容，下面我将举一个例子来说明如何选择一个多边形对一个很少数量多边形的集合进行分割。

       图1.5

在上面的例子中无论你选择多边形1、6、7还是多边形8进行渲染时都不会分割任何其它的多边形，换句话说也就是所有的其它多边形都位于这些多边形的“正面”。

关于分割时选择产生多边形最少的分割面另外一个不太好的原因是大多数时候它所产生的层次树通常是不平衡的，而一个平衡的层次树在运行的时候通常比不平衡的层次树性能更好。

当获得最佳的分割面后伴随着必然产生一些被分割的多边形，如何对被分割的多边形进行处理呢，这里有两个方法：

1. 建立一个带叶节点的二叉树，这意味着每一个多边形将被放在叶节点中，因此每一个被分割的多边形也将被分开放在二叉树的一边。

2. 另外一个方法是将被分割的多边形保存到公共节点中，对每一个子树重复这个过程直到每一个叶节点都包含了一个“凸”多边形集合为止。

产生带叶节点的BSP树的算法如下：

l 函数GENERATE-BSP-TREE

l 参数:

l Node – 欲建立的类型为BSPTreeNode的子树。

l PolygonSet – 建立BSP-tree的多边形集合。

l 返回值:

l 保存到输入的父节点中的BSP-tree。

l 功能:

l 对一个多边形集合产生一个BSP-tree。

GENERATE-BSP-TREE (Node, PolygonSet)

1 if (IS-CONVEX-SET (PolygonSet))

2 Tree = BSPTreeNode (PolygonSet)

3 Divider = CHOOSE-DIVIDING-POLYGON (PolygonSet)

4 PositiveSet = {}

5 NegativeSet = {}

6 for each polygon P1 in PolygonSet

7 value = CALCULATE-SIDE (Divider, P1)

8 if(value = INFRONT)

9 PositiveSet = PositiveSet U P1

10 else if (value = BEHIND)

11 NegativeSet = NegativeSet U P1

12 else if (value = SPANNING)

13 Split_Polygon10 (P1, Divider, Front, Back)

14 PositiveSet = PositiveSet U Front

15 NegativeSet = NegativeSet U Back

16 GENERATE-BSP-TREE (Tree.RightChild, PositiveSet)

17 GENERATE-BSP-TREE (Tree.LeftChild, NegativeSet)

算法分析

函数CHOOSE-DIVIDING-POLYGON的时间复杂度为O(n2 lg n)，除非出现递归调用否则它将控制其它的函数，如果我们假设对多边形集合的分割是比较公平的话，那么我们可以通过公式来对函数GENERATE-BSP-TREE的复杂度进行表达：

T(n) = 2T(n/2) + O(n2 lg n)

通过公式我们可以知道这个函数的复杂度为Q (n2 lg n)。这里n为输入的多边形集合的多边形数量。

下面我要用一个例子来演示如何产生一个BSP-tree。下面的结构是一个多边形的原始集合，为了表示方便对每一个多边形都进行了编号，这个多边形集合将被分割为一个BSP-tree。

             图1.6

为了能够运行这个算法我们必须对常量MINIMUMRELATION和MINRELATIONSCALE进行赋值，在实际运行中我们发现当MINIMUMRELATION=0.8而MINRELATIONSCALE=2时可以获得比较好的结果。但是你也可以对这些数值进行试验来比较一下，通常当常数MINIMUMRELATION比较大时获得的层次树会比较平衡但同时分割产生的多边形也会大量增加。在上图显示的多边形集合并不是一个“凸”的，因此首先我们需要选择一个合适的分割面。在快速的对上面的结构进行一下浏览后我们可以知道多边形（1、2、6、22、28）不能被用来作为分割面，这是因为它们定义了包含所有多边形集合的外形。但是其它的多边形都可以作为候选的分割面。分割产生的多边形最少同时分割为两个子集合的多边形数目之比为最佳的多边形是16与17，它们位于同一条直线上同时并不会分割任何的多边形。而分割后的子集合的多边形数目也是一样的，都是“正面”为13而“反面”为15。让我们选择多边形16作为分割面，那么分割后的的结构如下：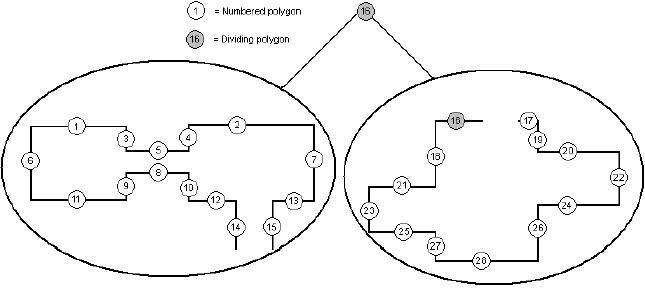

                         

 图1.7

现在从图1.7我们可以看到无论是左子树还是右子树都没有包含“凸”多边形集合，因此需要对两个子树继续进行分割。

在左子树中多边形1、2、6、7作为多边形集合的“凸边”不能用做分割面，而多边形4、10在同一条直线上同时没有分割任何多边形，而分割后的多边形子集合：“正面”为8而“反面”为7非常的平衡，我们选择多边形4为分割面。

在右子树中多边形16、17、22、23、28不能作为分割面，而多边形18、19、26、27虽然没有分割任何多边形但是分割后的多边形子集合：“正面”为11而“反面”为3，3/11这个比值小于最小比值0.5因此我们需要寻找其它更适合的多边形。多边形20、21、24、25都只分割了一个多边形，但是多边形21看起来分割后的结果更合理，在分割过多边形22后多边形子集合的结果为：“正面”为8而“反面”为6。

下图显示了操作后的结果：

                 图1.8

在图中每一个子集合还不是一个“凸”集合，因此需要继续进行分割，按照上面的法则对图1.8所示的结构进行分割后，结果如下：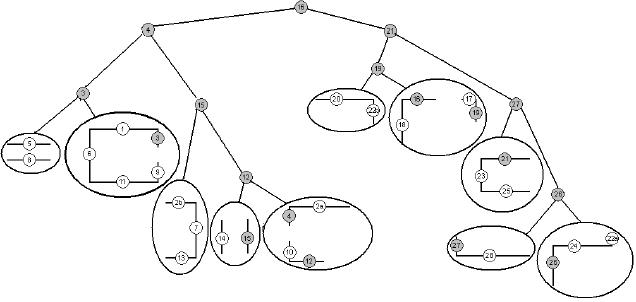

                       

图1.9

上图显示了最后的结果，这可能不是最优的结果但是我们对它进行处理所花费的时间并不太长。

渲染BSP

现在我们已经建立好一个BSP树了，可以很容易对树中的多边形进行正确的渲染，而不会产生任何错误。下面的算法描述了如何对它进行渲染，这里我们假设函数IS-LEAF的功能为给定一个BSP节点如果为叶节点返回真否则返回假。

函数DRAW-BSP-TREE

参数:

l Node – 被渲染的节点。

l Position – 摄象机的位置。

l 返回值:

l None

l 功能:

l 渲染包含在节点及其子树中的多边形。

DRAW-BSP-TREE (Node, Position)

1 if (IS-LEAF(Node))

2 DRAW-POLYGONS (Node.PolygonSet)

3 return

 

l 计算摄象机包含在哪一个子树中。

4 Side = CLASSIFY-POINT (Node.Divider, Position)

l 如果摄象机包含在右子树中先渲染右子树再渲染左子树。

5 if (Side = INFRONT || Side = COINCIDING)

6 DRAW-BSP-TREE (Node.RightChild, Position)

7 DRAW-BSP-TREE (Node.LeftChild, Position)

 

l 否则先渲染左子树。

8 else if(value = BEHIND)

9 DRAW-BSP-TREE (Node.LeftChild, Position)

10 DRAW-BSP-TREE (Node.RightChild, Position)

用这个方法进行渲染并没有减少渲染到屏幕上的多边形数量，由于一个场景可能包含成百上千个多边形因此这个方法并不是很好的解决方案。通常情况下有大量的节点和多边形并没有处于摄象机的视野范围之内，它们并不需要被渲染到屏幕上，如何查找这些不可见的节点和多边形防止它们渲染到屏幕上呢，隐藏面剔除就是为了解决这个问题而提出一项技术，在下一节中我们将对这项技术进行详细的阐述。

 

第三章 隐藏面剔除

    对不可见物体进行剔除是游戏行业为了满足提高画面渲染速度的要求而产生的一项技术，就是在硬件加速技术飞跃发展的今天，虽然现在已经可以完成许多在过去被认为是不可能实现的工作，但是对于隐藏面进行剔除仍是加速图形渲染的一项重要技术。通常当一个游戏运行的时候，它最少需要以每秒30帧的速度运行。在几年前这意味着如果每一帧你渲染的带纹理的多边形数量超过5000个就被认为是不可接受的，而现在几乎所有的商业显卡每一秒都可以渲染几千万个多边形。可是现在仍然需要使用隐藏面剔除这项技术，这是为什么呢？显而易见，对不可见物体渲染以后将会被可见物体遮挡住，这样做无谓的浪费了显卡的带宽，但是同时它也增加了场景的细节，使游戏画面看起来更加吸引人。现在的问题是多大程度上来剔除隐藏的多边形，象view frustum culling和portal渲染这样的技术来剔除一个不可见多边形是非常耗费时间的，用来去做这些计算的CPU时间可以用来完成其它诸如AI或碰撞检测这样的工作，因此开发一个隐藏面剔除算法必须注意到这一点。对于现在的游戏来说几乎没有一个是将每一个隐藏的多边形都进行剔除，而是剔除一个多边形的集合如一个节点或一个物体等等。对于一个单独的多边形它并不进行剔除，因此一个正确的隐藏面剔除方案是允许一定的重复渲染来适当的减少计算量。

    当建立一个FPS游戏时进行隐藏面剔除最通常的方法是使用portal渲染。这项技术可以非常充分的利用BSP的优点，但是请注意portal技术并不仅仅只能用于BSP中。Portal技术还可以用来产生一些特效如镜子和监视器等等。

Portal渲染

在这里我将介绍一下portal技术的原理，通常对于一个室内场景来说它可以被描述为由一个个“洞口”相互连接的“房间”组成，这里“洞口”被称为portal而“房间”被称为sector，通常sector被定义为一个“凸”的“闭合”的多边形集合，定义中的“凸”阅读过前面的内容你应当已经能很好的理解了，而“闭合”是什么意思呢？它意味着在sector内部任意连接两个顶点做一条线段，这条线段不会和其它的多边形相交。换句话说如果你想在sector内部任意画一条线段通到sector的外部必定与组成sector的多边形相交。这也意味着连接每一个sector的“洞口”必须被一个组成portal的多边形所填充，而对于放置portal多边形来说你既可以手工放置也可以由程序自动产生，在我讲解这项技术之前我必须提醒一下，由于硬件加速Z缓冲的出现对sector必须为“凸”的限制已经消除，因此有许多游戏引擎已经不再遵守这个标准，但是在这里我还是要对过去的方法进行一下介绍。

一个portal引擎的基本方法是当你通过一个指定观察位置的可视平截体（view frustum）进行渲染时，如果一个portal出现在可视范围内，那么portal将对可视平截体进行剪切，这样与其相连的sector将会通过一个观察位置相同但已经改变过的可视平截体进行渲染。这是一个非常简单而且非常适合进行递归调用的方法，由于可视平截体被portal进行了精确的限制，因此被隐藏的物体可以很简单进行剔除。下面的例图显示了一个portal引擎中的可视平截体是如何被剪切的。

                

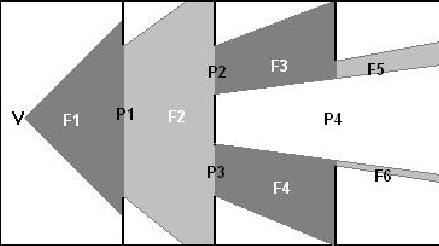图6.10

在图6.10中观察者的位置位于V，而初始的可视平截体为F1，当它通过一个portal多边形P1后被P1剪切产生新的可视平截体F2，接着当它通过portal多边形P2、P3后F2被剪切为F3、F4，而F3通过P4后被剪切为F5而F4被剪切为F6。观察这个过程我们可以发现portal技术非常适合进行递归调用。

接着需要考虑的是如何对物体进行拣选剔除，通常对于所有的3D引擎来说都需要通过一系列步骤来加速这个处理过程，回忆一下前面讲解的内容，这个过程首先要计算出物体的“最大包围球”或是“最大包围盒”，它是包含了物体所有顶点的最小包围体，接着用包围体来和“可视平截体”每一个剪切面进行碰撞检测，如果包围体位于每一个剪切面的“反面”那么物体将不会进行渲染，下图显示了这个过程：

         

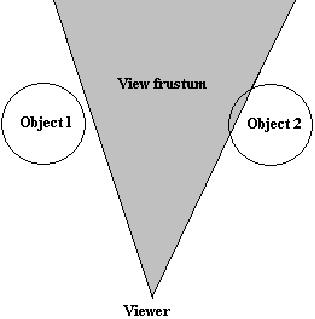图6.11

图中物体1位于右剪切面的“正面”但位于左剪切面的“反面”因此它将不会被渲染，而物体2不仅位于左剪切面的“正面”而且有一部分位于右剪切面的“正面”因此将会被渲染出来。

Portal技术最初的想法是通过剪切多边形来保证只有物体可见的部分被渲染出来，也就是无效渲染的多边形数量为0。但是现在这种想法被认为不是很理想，因为它无谓的浪费了处理时间。但是由于一个多边形在递归循环过程中将被遍历多次因此我们需要知道在渲染场景时它是否已经被渲染过，一个较好的方法是使用一个帧数来标识这个多边形，这样可以很容易的来描述这个多边形在上一帧是否被渲染过。再看一下图6.10中最右边的墙，它同时通过F5和F6来进行渲染，通过对它进行标识我们可以知道它是否被渲染过，否则就会产生Z缓冲错误。

为了便于在portal引擎中进行渲染我们需要对“可视平截体”进行一下定义，一个“可视平截体”是一个保存了多个剪切面的结构，每一个剪切面的法线都将指向“可视平截体”的内部，因此在它内部将产生一个闭合的锥体。下面的算法显示了如何计算一个多边形是否包含在“可视平截体”的内部。在这个算法中我们使用了一个函数CLASSIFY-POINT，它使用一个剪切面和一个点作为输入参数。

l 函数INSIDE-FRUSTUM

l 参数:

l Frustum – 用于检测多边形是否位于其中的“可视平截体”。

l Polygon – 用于检测的多边形。

l 返回值:

l 多边形是否位于“可视平截体”的内部。

l 功能:

l 使用“可视平截体”的每一个剪切面来对多边形的每一个顶点进行检测，如果所有的顶点都位于所有剪切面的“正面”，那么多边形处于“可视平截体”的内部。

 

INSIDE-FRUSTUM (Frustum, Polygon)

1 for each point Pt in Polygon

2 Inside = true

3 for each plane Pl in Frustum

4 if (CLASSIFY-POINT (Pl, Pt) <> INFRONT)

5 Inside f false

6 if (Inside)

7 return true

8 return false

在一个portal引擎中它的主渲染函数可以简单的用下面的方法来实现。

函数RENDER-PORTAL-ENGINE

参数:

Sector – 观察者所处的sector。

ViewFrustum – 当前的“可视平截体”。

返回值:

None

功能:

渲染portal引擎中的多边形，场景被描述为由多个portal连接的sectors所组成。

RENDER-PORTAL-ENGINE (Sector, ViewFrustum)

1 for each polygon P1 in Sector

2 if (P1是一个portal and INSIDE-FRUSTUM (ViewFrustum, P1))

3 NewFrustum = CLIP-FRUSTUM (ViewFrustum, P1)

4 NewSector = 获得由当前sector通过portal P1相连接的sector

5 RENDER-PORTAL-ENGINE (NewSector, NewFrustum)

6 else if (P1任然没有被渲染)

7 draw P1

8 return

如何放置portal

正如我前面提到的在一个portal引擎中最大的问题就是如何放置portal，如果手工来放置它的话非常花费时间，同时要求地图的设计者有熟练的技巧。因此一个良好的自动放置portal的算法非常有必要，在这里我将要介绍一下关于这方面的几个解决方案，这些方案都使用了BSP。

我介绍的第一个解决方案是由瑞典DICE公司的Andreas Brinck提出的，它的原理非常简单，观察一下一个完整的BSP层次树，可以发现这样一个现象，对于每一个portal来说它必定与BSP层次树中由分割多边形定义的分割面位置相同，因此在相同的位置上我们可以在分割面之外建立一个portal多边形，portal多边形被初始化为一个矩形，这个矩形的大小将超过portal所处的BSP节点的“最大包围盒”的大小，接着将portal多边形放入包含它的节点所位于的子树中，当节点不是叶节点时，那么portal将继续被传送到节点的子树中，这样子节点中的分割面将对它进行分割，而当包含它的节点为叶节点时，它也会被节点中的多边形进行剪切，因为portal初始化的大小超过了节点的范围。当portal被分割后，被分割的两个部分会继续传送到最顶层的节点重复这个过程，而当portal不需要进行分割时，根据它所处于分割面的位置来放置到相应的子节点中，如果位于分割面的“正面”它将被放置在右子树中，而当它位于分割面的“反面”将被放置于左子树中。如果portal正好位于分割面之上它将同时放在左右子树中。

为了方便方便将所有的portal放置到BSP中我们需要定义如何对一个多边形进行分割，为了方便使用我们假设完成这个功能的函数为INTERSECTION-POINT，它将返回一个面与一个线段的交点。

l 函数CLIP-POLYGON

l 参数:

l Clipper – 去分割其它多边形的多边形或面。

l Polygon – 被分割的多边形。

l 返回值:

l 被分割后的两个部分。

l 功能:

l 由指定的分割面来分割多边形。如果多边形没有被分割将会返回一个空的多边形。

CLIP-POLYGON (Clipper, Polygon)

1 RightPart = {}

2 LeftPart = {}

3 for each point edge E in Polygon

4 Side1 = CLASSIFY-POINT (Clipper, E.Point1)

5 Side2 = CLASSIFY-POINT (Clipper, E.Point2)

6 if (Side1 <> Side2 and

Side1 <> COINCIDING and

Side2 <> COINCIDING)

7 Ip = INTERSECTION-POINT (Clipper, E)

8 if (Side1 = INFRONT)

9 RightPart = RightPart U E.Point1

10 RightPart = RightPart U Ip

11 LeftPart = LeftPart U Ip

12 LeftPart = LeftPart U E.Point2

13 if (Side1 = BEHIND)

14 LeftPart = LeftPart U E.Point1

15 LeftPart = LeftPart U Ip

16 RightPart = RightPart U Ip

17 RightPart = RightPart U E.Point2

18 else

19 if (Side1 = INFRONT or Side2 = INFRONT or

Side1 = COINCIDING and Side2 = COINCIDING)

20 RightPart = RightPart U E.Point1

21 RightPart = RightPart U E.Point2

22 if (Side1 = BEHIND or Side2 = BEHIND)

23 LeftPart = LeftPart U E.Point1

24 LeftPart = LeftPart U E.Point2

25 return (RightPart, LeftPart)

现在我们可以定义如何在一个BSP层次树中对portal进行分配了，在算法中portal被初始化为一个大于BSP根节点“最大包围盒”的多边形。

l 函数PLACE-PORTALS

l 参数:

l PortalPolygon – 放置到BSP中的多边形。

l Node – 我们当前遍历的节点。

l 返回值:

l None

l 功能:

l 放置一个portal多边形到BSP层次树中，如果需要的话对它进行剪切。这个函数将会产生一个节点将由portal连接而每一个节点将包含一个portal多边形列表的BSP层次树。

PLACE-PORTALS (PortalPolygon, Node)

1 if (IS-LEAF (Node))

 

l 将portal和节点中的每一个多边形进行检测。当portal所包含的多边形和由一个多边形定义的面相交时它将被这个面进行分割，分割后的两个部分将被重新传送到最顶层的节点中继续进行检测。

2 for (each polygon P2 in Node)

3 IsClipped = false

4 if (CALCULATE-SIDE (P2, PortalPolygon) = SPANNING)

5 IsClipped = true

6 (RightPart, LeftPart) = CLIP-POLYGON (P2, PortalPolygon)

7 PLACE-PORTALS (RightPart, RootNode)

8 PLACE-PORTALS (LeftPart, RootNode)

9 if (not IsClipped)

10 从当前节点中将portal的多边形剔除，因为它的位置和节点中一个多边形的位置相同。

l 参考下面的描述。

11 添加当前节点到portal多边形所连接的节点集合中。

12 else

13 if (当前节点的分割多边形没有放置在树中)

14 建立一个多边形P，它的大小将超过包含当前节点所有多边形的最大包围盒的范围，并且和分割多边形的位置相同。

15 PLACE-PORTALS (P, Node.LeftChild)

16 PLACE-PORTALS (P, Node.RightChild)

17 Side = CALCULATE-SIDE (Node.Divider, PortalPolygon)

18 if (Side = POSITIVE)

19 (RightPart, LeftPart) = CLIP-POLYGON(P2, PortalPolygon)

20 PLACE-PORTALS (RightPart, RootNode)

21 PLACE-PORTALS (LeftPart, RootNode)

22 if (Side = POSITIVE or COINCIDING)

23 PLACE-PORTALS (PortalPolygon, Node.RightChild)

24 if (Side = NEGATIVE or COINCIDING)

25 PLACE-PORTALS (PortalPolygon, Node.LeftChild)

下面我将对算法中的第10行进行一下解释，当剔除和当前节点中一个多边形位置相同的portal多边形部分将会产生什么样的结果。参考一下图6.12。

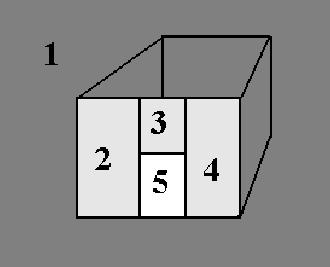图6.12

在图6.12中一个portal已经到达了一个叶节点，图中灰色的区域是是portal多边形在遍历BSP树过程中被剔除的区域称它为1。而图中标注为2、3、4的亮灰色部分是和portal多边形位置相重叠的多边形，因此这一部分的portal多边形也将会被剔除，而剩下的部分5将被用来做为一个portal。

在上面的算法第一次看的话会觉的非常复杂，但实际上它非常简单和容易理解，最终的结果就是每一个portal将会在两个节点上结束而对于任一个portal来说它必定可以和一个portal之间相互可见。在下面我将用一个实际的例子来解释一下这个算法。

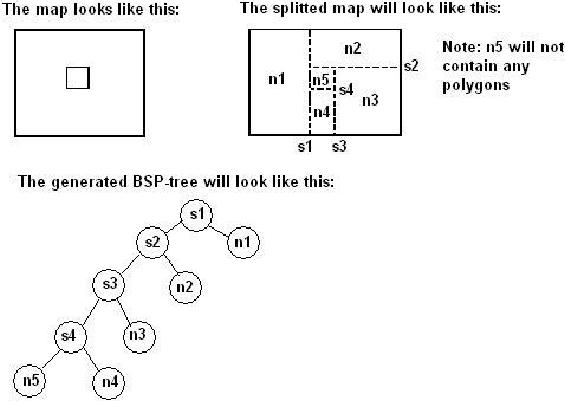图6.13

对于图6.13中的结构，需要进行下面的几步：

第一步，portal多边形s1进入节点n1中。

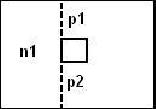    在节点n1中portal多边形s1将会被分割，因为它的一部分和节点中间的一个多边形位置相同，因此portal多边形s1将会被分割为两部分分别为p1、p2，重叠的部分被剔除。

第二步，p1、p2进入节点s2中。

在节点s2中由于p1位于分割面s2的“正面”，因此将和分割面s2一起被送入到节点n2中，而p2由于位于分割面s2的“反面”，因此将和分割面s2一起被送入到节点s3中。由于p1、p2没有和分割面相交因此这一步没有出现分割操作。

第三步，p1、s2进入节点n2中。

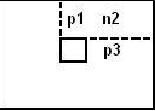在节点n2中n2被认可作为一个portal，因此在节点n1和n2中它不会再发生任何变化。而多边形p3的一部分将会被剔除，因为它的一部分和节点中间的一个多边形位置相同，在上一步中多边形s2也被送入到节点s3中，而在这里它又被称为p3。

第四步，p3和s3进入节点n3中。

在节点n3中多边形p3被认可为一个portal，而多边形s3的一部分因为和上面的原因一样被剔除，同时在这里它又被称为p4。

 

 

第五步，p2和p4进入节点s4中。

没有任何多边形要进行分割，因此多边形p2和p4将与s4一起被送入节点n4中，而s4将被单独送入节点n5中。

第六步，p2、p4和s4一起进入节点n4中。

无论是p2还是p4都不需要分割，但是由于s4和中间的一个多边形完全重叠因此将会被剔除。

 

 

第七步，结束，没有任何多边形进入节点n5中。

这个节点将没有portal，因为对于任何节点来说它都是不可见的，而从这个节点位置上将不会看见任何一个节点。

结果：

portal p1同时位于节点n1和n2中；

portal p2同时位于节点n1和n4中；

portal p1同时位于节点n2和n3中；

portal p1同时位于节点n3和n4中。

 

上面我所讲解的内容是建立一个简单的portal引擎所必备的功能，它能给我们提供一个较高的运行帧速。

PVS

    一个portal引擎虽然能够提供许多非常好的特性，但是它的结构太复杂。当你使用portal技术来构建一个游戏引擎时你会发现它存在许多问题，最大的一个问题是在渲染场景的每一帧都需要进行可视性检测，这会产生大量的多边形剪切操作，在场景非常复杂的情况下，运算的费用会非常的高，因此需要寻找一种技术来对场景中可视性检测进行预计算而不是在运行期间进行计算。PVS（Potentially Visible Set）可视性集合，就是为了解决这个问题而出现的一项技术，可以通过对BSP中每一个叶节点设置一个PVS，这个PVS保存了从第一个叶节点开始看到的叶节点集合，它不仅可以用来帮助加速场景渲染，还可以用来加速场景中光照运算和进行网络优化。

PVS是在场景进行预渲染时计算出来的，每一个BSP的叶节点都保存一个可视节点的集合，当对场景进行渲染时，摄象机所在的叶节点将被渲染，同时保持在PVS中的叶节点也将会被渲染出来，这里需要一些算法来避免场景重复渲染，由于今天硬件加速卡的发展，它所提供的硬件Z缓冲的大小已经可以方便的解决这个问题。

计算PVS

如果要求PVS必须在BSP的叶节点之间进行标准的光线跟踪计算，来查找一下在一个叶节点中任一个点是否在其它叶节点中可见。为了加速光线跟踪的计算，在每一个叶节点中必须指出一些典型的位置点来避免无谓的计算，现在的问题就是如何放置这些典型的点。

对于一个portal引擎的portal来说，典型点可以沿着树的分割面放置，这是因为只有在两个portal是相互开放的情况下才可以进行可视化检测。如果位于一个叶节点中间的一个点被从另一个叶节点发射出来的光线认为是可见的话，那么这条光线必然通过连接两个节点的portal，参考下图：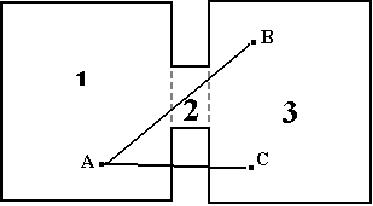

图6.14

在图6.14中我们可以看见如果在一个节点中的一个点可以从其它节点看见，那么视线必然通过两个节点相互连通的区域。这是非常明显的，如果视线被物体阻断的话那么两点之间必定不可见。因此将典型点放置在两个节点之间所开放的区域是非常合适的，下面描述的算法将在一个BSP树上放置典型点。对于这个函数需要一组帮助函数来把点放置在一个节点上，它们是

l DISTRIBUTE-POINTS (Node) 这个函数将按照一定的间隔沿着给定节点的分割面来放置点，点的位置会处于节点包围盒的内部。它将返回一个点的集合，复杂度为O(xy)，这里x为节点包围盒内分割面的宽度，而y为高度。

l CLEANUP-POINTS (Node, PointSet) 从点的集合中剔除不合格的点，这些点可能和节点中的一个多边形位置相同，也可能是位于节点包围盒的外部。函数的复杂度为O(np)，这里n为节点中多边形的数量而p为集合中点的数量。

l 函数 DISTRIBUTE-SAMPLE-POINTS

l 参数:

l Node – 当前我们遍历的节点。

l PointSet – 放置到给定节点子树中的点的集合。

l 返回值:

l None

l 功能：

l 沿着给定节点的分割面放置点。它将按照分割面的位置来对输入的点进行检测，如果这些点和节点中的一个多边形位置相同，或者位于节点包围盒的外部那么将会被剔除。新产生的点将会被添加到左、右两个集合中，当一个点的集合遍历到一个叶节点时那么它就是这个叶节点的典型点。

DISTRIBUTE-SAMPLE-POINTS (Node, PointSet)

1 CLEANUP-POINTS (Node, PointSet)

2 if (IS-LEAF (Node))

3 设置点的集合为当前节点的典型点。

4 else

5 RightPart = NewPoints

6 NewPoints = DISTRIBUTE-POINTS (Node)

7 RightPart = NewPoints

8 LeftPart = NewPoints

9 for each point P in PointSet

10 Side = CLASSIFY-POINT (Node.Divider, P)

11 if (Side = COINCIDING)

12 RightPart = RightPart U P

13 LeftPart = LeftPart U P

14 if (Side = INFRONT)

15 RightPart = RightPart U P

16 if (Side = BEHIND)

17 LeftPart = LeftPart U P

18 DISTRIBUTE-SAMPLE-POINTS (Node.LeftChild, LeftPart)

19 DISTRIBUTE-SAMPLE-POINTS (Node.RightChild, RightPart)

算法分析

    每一次调用这个函数的复杂度为O(np + xy)（参考函数CLEANUP-POINTS和

DISTRIBUTE-POINTS），为了计算完整的复杂度我们可以用下面的公式来表示（我们假设典型点的集合同时分布在两个集合之中）：

T(n) = 2T(n/2) + O(np + xy)

这个函数第一次调用时将会从BSP树的根节点开始并会传入一个空的集合。换句话说它是按照下面的方法进行的，它是从被BSP树根节点所定义的分割面上的点开始的，由于一个面的大小没有限制因此也会有无限个典型点，因此就需要对典型点进行限制，这个现在就是根节点的包围盒。

在根节点上获得合格的典型点后需要把所有的点发送到根节点的两个子树中，当一个典型点的集合进入一个节点后会被分割为两个部分，一个部分包含了所有位于节点分割面的“正面”的点，而另一部分包含了所有位于节点分割面的“反面”的点。而位于分割面上的点将会同时放在两个集合中。接着“正面”集合将会被传入到右子树中而“反面”集合将会被传入到左子树中。重复这个过程直到进行到叶节点时结束，在这些操作后每一个叶节点将包含一个典型点的集合，这些点都位于节点所连通的地方。

如果我们现在在这个阶段对每一个节点进行光线跟踪那么是非常耗费时间的，但是如果我们知道叶节点是与哪一个节点相连的，那么这个过程将会变的简单，因为这样可以减少一些不必要的光线跟踪运算。查找相互连接的叶节点非常简单，可以通过检测每一个叶节点的典型点来查找，如果同时有两个节点共享一个点那么这两个节点必然是相互连通的，因为在遍历BSP树放置典型点的过程中，点不是没有放置到节点上就是同时放置在两个节点上。当我们知道哪些节点是相互连通的，就可以定义进行光线跟踪的算法了，不过首先我们需要定义一些帮助函数。

为了方便进行光线跟踪我们需要一些基本的光线跟踪函数，BSP树是非常适合进行光线跟踪的结构，因为大部分不可见的区域通过BSP树可以很简单的剔除掉，不用进行遍历，因此花费的时间也非常少。我们需要的函数如下：

POLYGON-IS-HIT (Polygon, Ray) 返回光线是否和多边形相交。

RAY-INTERSECTS-SOMETHING-IN-TREE (Node, Ray) 返回光线是否和节点中的子树相交。

INTERSECTS-SPHERE (Sphere, Ray) 返回光线是否和球体相交。

CREATE-RAY (Point1, Point2) 通过两个点来建立一条光线。

上面的函数RAY-INTERSECTS-SOMETHING-IN-TREE是一个非常有趣的函数，因为它显示了一些BSP树的优点，同时也显示了如何使用BSP树来加速光线跟踪的处理。它是一个递归函数，首先在树的根节点上使用，伪算法如下：

l 函数RAY-INTERSECTS-SOMETHING-IN-TREE

l 参数：

l Node – 用来进行跟踪的节点。

l Ray – 用来进行求交的光线。

l 返回值：

l 光线是否和节点中的物体相交。

l 功能：

l 检测光线是否与给定节点极其子树中的物体相交。

RAY-INTERSECTS-SOMETHING-IN-TREE (Node, Ray)

1 for each polygon P in Node

2 POLYGON-IS-HIT (P, Ray)

3 startSide = CLASSIFY-POINT (Ray.StartPoint, Node.Divider)

4 endSide = CLASSIFY-POINT (Node.EndPoint, Node.Divider)

l 如果光线和节点的分割面相交或和分割面的位置重叠，对节点的两个子节点进行检测。

5 if ((startSide = COINCIDING and endSide = COINCIDING) or

startSide <> endSide and startSide <> COINCIDING and

endSide <> COINCIDING)

6 if (RAY-INTERSECTS-SOMETHING-IN-TREE (Node.LeftChild, Ray))

7 return true

8 if (RAY-INTERSECTS-SOMETHING-IN-TREE (Node.RightChild, Ray))

9 return true

l 如果光线只位于分割面的“正面”对节点的右子树进行检测。在if语句中使用or操作符是因为光线的一个端点可能与分割面的位置重叠。

10 if (startSide = INFRONT or endSide = INFRONT)

11 if(RAY-INTERSECTS-SOMETHING-IN-TREE (Node.RightChild, Ray))

12 return true

l 如果光线只位于分割面的“反面”对节点的左子树进行检测。在if语句中使用or操作符是因为光线的一个端点可能与分割面的位置重叠。

13 if (startSide = BEHIND or endSide = BEHIND)

14 if (RAY-INTERSECTS-SOMETHING-IN-TREE (Node.LeftChild, Ray))

15 return true

l 光线没有和任何物体相交，返回到上一层。

16 return false

算法分析

最坏的情况是光线遍历了BSP树中每一个节点，这样光线将与节点中每一个单独的多边形进行检测，这时函数的复杂度将为O(n)，这里n为BSP树中所有多边形的数量。一般情况下光线并不会检测树中的每一个节点，这样将会大大减少进行检测的多边形数量。最佳的情况是光线被限制在一个节点中，这时函数的复杂度接近于Ｏ(lg n)．这取决于BSP树的结构大小。

l 函数CHECK-VISIBILITY

l 参数：

l Node1 – 开始处的节点。

l Node2 – 结束处的节点。

l 返回值：

l Node2是否可以被node1看见。

l 功能：

l 在两个叶节点的典型点之间进行跟踪，检测两个节点之间是否可见。

CHECK-VISIBILITY (Node1, Node2)

1 Visible = false

2 for each 典型点P1 in Node1

3 for each 典型点P2 in Node2

4 Ray = CREATE-RAY (P1, P2)

5 if(not RAY-INTERSECTS-SOMETHING-IN-TREE(Node1.Tree.RootNode,

Ray)

6 Visible = true

7 return Visible

算法分析

函数CHECK-VISIBILITY非常耗费时间，当我们在两个叶节点之间进行光线跟踪来检测两者之间是否可见时，我们不得不从Node1的每一个典型点开始对Node2的每一个典型点进行跟踪，最坏的情况是每一次跟踪都将对树中所有的多边形进行检测，这时函数的复杂度O(s1 s2 p)，这里s1为Node1中典型点的数量，s2为Node2中典型点的数量，p为树中多边形的数量。通常它的性能是比较好的，接近于O(s1 s2 lg p)。

l 函数TRACE-VISIBILITY

l 参数：

l Tree – 去进行光线跟踪的BSP-tree。

l 返回值：

l None

l 功能：

l 对于树中每一个叶节点，它将进行光线跟踪运算来检测和它相连的节点的可见性。每一个被发现是可见的节点将会被添加到当前节点的PVS中。当一个叶节点发现是可见的，我们还要对和它相连的节点进行光线跟踪运算来检测可见性。

TRACE-VISIBILITY (Tree)

1 for (each 树中的叶节点L)

2 for (each 和叶节点L相连的叶节点C)

3 添加节点C到节点L的PVS中

4 for (each 树中的叶节点L1)

5 while (在叶节点L的PVS中存在一个叶节点L2，它所连接的节点没有进行可见性检测)

5 for (each 连接到节点L2中的叶节点C)

6 if (节点C没有位于节点L1的PVS中 and

CHECK-VISIBILITY (L1, C))

7 添加节点C到节点L1的PVS中

7 添加节点L1到节点C的PVS中

算法分析

如果我们没有使用根据叶节点的相连情况来进行处理的优化技术，那么必须对树中的每一个叶节点进行检测，这时函数的复杂度为O(n2)，这里n为树中叶节点的数量。要对上面的算法估计一个对处理过程提高了多少性能的具体数值非常困难，因为它依赖于所处理的结构的大小。对于每一个叶节点与其它节点都是可见的结构，这个算法不会做任何优化。对于每一个叶节点只有一到二个可见的节点的结构，这个算法将会产生非常大优化，它的复杂度接近与O(n)。

现在在一个设计良好的地图上所产生的结构在每一帧上将会避免检测大量的多边形。一个设计良好的地图在建立时将会考虑物体的可见性，这意味着应尽可能的在地图中放入一些能障碍视线的物体，如墙壁等。如果在地图中包含一个有大量细节的大房间，那么在上面的算法中（或在一个portal引擎中）进行的隐藏面剔除工作对它不会产生任何效果。这时我们需要使用其它类似于LOD这样的技术来进行多边形剔除。

静态物体

考虑一下这样的场景，一个球体位于一个立方体的中心，如果用BSP对它进行渲染那么将会产生大量的节点，并会产生大量的分割多边形，这是因为在球体上的每一个多边形都会送入到叶节点中。如果球体有200个多边形当渲染时就会产生200个叶节点的BSP树。这样做非常影响运行的速度，因此必须寻找一个方法来避免这种现象的发生。

为了解决这个问题地图的设计者可以选择组成地图的几何体，在上面的例子中也就是立方体，接着将剩余的物体做为静态物体，它们将不会用来对BSP树进行渲染或进可见性检测，但是它们会参与到地图的光照运算当中去。当进行可见性运算时每一个静态物体会被添加到BSP树中，每一个静态物体的多边形将会被添加到BSP树中，这个过程如下：

l 函数PUSH-POLYGON

l 参数：

l Node – 多边形当前所在的节点。

l Polygon – 将被添加的多边形。

l 返回值：

l None

l 功能：

l 将多边形添加到树中。如果多边形的一些点与节点的分割面相交将会被分割。分割后的部分将会被继续向下传送。当一个多边形进入一个叶节点后它将被添加到叶节点的多边形集合中。

PUSH-POLYGON (Node, Polygon)

1 if (IS-LEAF (Node))

2 Node.PolygonSet = Node.PolygonSet U Polygon

3 else

4 value = CALCULATE-SIDE (Node.Divider, Polygon)

5 if (value = INFRONT or value = SPANNING)

6 PUSH-POLYGON (Node.RightChild, Polygon)

7 else if (value = BEHIND)

8 PUSH-POLYGON (Node.LeftChild, Polygon)

9 else if (value = SPANNING)

10 Split_Polygon28 (P1, Divider, Front, Back)

11 PUSH-POLYGON (Node.RightChild, Front)

12 PUSH-POLYGON (Node.LeftChild, Front)

PUSH-POLYGON是一个递归函数，它将一个多边形添加到BSP树中，这个函数对每一个静态物体的每一个多边形都会调用一次，

在这个过程处理之后叶节点可能不再成为一个“凸”集合，这在进行碰撞检测时可能会产生一些问题，后面的内容将会对这个问题进行阐述。

 第四章 RADIOSITY

关于Radiosity的算法最早是由Goral、Cindy M、Torrance、Kenneth E、Greenberg、Donald P、Battaile和Bennett在论文《Modelling the interaction of light between diffuse surfaces》提出的。他们使用Radiosity来模拟能量在漫反射表面之间进行传送，漫反射表面对照到表面上的光线在所有的方向上都进行相同的反射，和它相反的是镜面反射表面，它只在反射方向上传播反射光。由于漫反射表面的这个特性，这就意味着对于所有的观察角度而言看起来表面都是相同的，这样对于场景中的每一个表面只需要进行一次光照运算，而且可以在场景的预渲染时进行，因此这项技术被大量的3D游戏所采用。

下面我再简短的讲解一下Radiosity是如何工作的，而将主要的精力放在如何使用BSP树来加速Radiosity的计算，对于Radiosity的详细介绍请参考前面的章节。Radiosity技术是设计用来使场景中光照看起来更加真实和光滑，如果我们使用一个一直向前传播而不考虑反射的光照模型，那么当场景中的灯光照亮场景中的物体时，并不会计算远处经过反射过来的光线，这样场景中的阴影看起来非常尖锐而物体表面也看起来非常不真实。为了使用radiosity技术我们需要把场景分割成一块一块很小的部分，每一部分我们称它为patch，每一个patch都有一个初始化的能量级别，如果它不是一个灯光这样的发光体的话通常为0，有许多方法来分配场景中的能量，这里我们将要使用的方法称为交互式radiosity。这个方法的过程是我们从场景中未发送能量的级别最高的patch开始发送能量，能量经过传递后将不再发送能量的patch的等级设为0，重复这个过程直到场景中的每一个patch的能量等级都小于一个预定值为止。

当能量从一个patch（j）开始发送到另一个patch（i）时我们使用下面的公式：

Bi = Bi + Bj * Fij * Ai / Aj

这里Bi = patch（i）的能量级别     Bj = patch（j）的能量级别 

    Ai= patch（i）的作用区域    Aj = patch（j）的作用区域

    Fij = patch（i）与patch（j）之间的系数

在公式中系数Fij是由以下公式来确定的：

Fij = (cos qi * cos qj) / d2 * Hij

这里Fij = patch（i）与patch（j）之间的系数

qi = patch（i）与patch（j）法线之间的夹角

qj = patch（i）与patch（j）法线之间的夹角

d = patch（i）与patch（j）之间的距离

Hij = patch（i）与patch（j）之间的可见性系数。如果在两个patch之间只有一条光线可以跟踪，这个值为1，如果没有光线可以跟踪为0。一般情况下由于每一个patch都不是一个点而是一个区域，因此光线有很多条。

从上面的公式中我们可以看到在场景中进行radiosity计算是非常耗费时间的。这个函数的复杂度为O(n3)，这里的n为场景中patch的数量。由于对于场景中每一个patch你需要发送最少一条光线到其它patch上，因此需要对场景中的几乎所有的多边形都进行光线跟踪计算。在上面的公式中系数H的计算非常耗费时间，下面我们将看一下如何在BSP树中对它的计算进行优化。

 

    BSP树中的radiosity计算

在进行场景中的光照计算之前需要把场景中的面分割为patch，一个方法是在开始的时候设定每一个patch为预定的大小，当计算每一个patch的能量时，如果在patch上的能量足够大，对这个patch进行分割。不过这个方法是非常耗费时间的，因此必须寻找一个更好的方法来通过BSP树对计算进行优化。

在radiosity的一般算法中场景中的每一个光源都被看作为一个或多个patch，这里我们可以改进一下，将每一个光源放在它所位于的叶节点中，接下来每一个光源都发送自己的能量到场景中所有的patch上，当这个过程完成后radiosity计算也就结束了。为了使最后的结果看起来更好可以使用一种称为“渐进精选”（progressive refinement）的技术来对这个方法进行很小的修改。在每一次过程中，叶节点中具有高能量的patch将发送能量到其它低能量的patch上，这样做的结果是高亮度的patch将发送能量到处于阴影中patch上。这是因为在实际生活中并没有真正黑暗的地方，它多多少少要获得一些其它物体反射过来的光亮。

由于计算非常耗费时间需要做一下优化，使用渲染BSP树时获得的PVS信息可以在选择哪些patch将接受能量时剔除一些无用的计算。因为在计算PVS时使用了相同的方法来进行光线跟踪。

通过场景来分配能量的算法如下：

l 函数RADIOSITY

l 参数：

l Tree – 进行radiosity计算的BSP树。

l 返回值：

l None

l 功能：

l 在场景中的patch之间发送能量。

RADIOSITY (Tree)

1 for(each leaf L in Tree)

2 for(each light S in L)

3 for(each leaf V that is in L’s PVS)

4 Send S’s energy to the patches in V

l 下面语句5是为了让地图编辑者在任何时候都可以检查场景渲染的效果，如果他感到看起来已经足够好了可以中断能量的传播。

5 while(not looks good enough)

6 for(each leaf L in Tree)

7 for(each leaf V that is in L’s PVS)

8 Send energy from the patch with the most unsent energy in L

to all patches in V.

复杂度分析

这个函数的运算费用实在是太高昂了，可以称为时间杀手，在最坏的情况下每一条光线将不得不检测场景中的每一个多边形，此时复杂度为O(n3)，这里n为树中patch的数量。一般情况下由于进行了优化可以减少大量的计算，但是减少多少并不能计算出来，因为这依赖于树结构的复杂度。

上面的函数给出了一个充分利用BSP树的优点来加速场景光照运算的方法，尤其是可以显著的减少光线跟踪的计算量，而且地图设计者可以来决定当场景渲染时如果渲染的效果可以接受中断渲染循环。这对地图的预渲染实在是太方便了，运行的时间可以根据渲染的效果来决定。

第五章 BSP树渲染概要

现在我们已经描述了BSP引擎中完成预处理部分所需的步骤。接下来是将场景渲染成BSP树的算法：

l 函数RENDER-SCENE

l 参数：

l Scene – 被渲染的场景

l 返回值：

l 一个BSP树。

l 功能

l 预渲染来获得一个包含场景信息的BSP树。

RENDER-SCENE (Scene)

l 使用描述场景中图元的物体来渲染BSP树。

1 GeometryPolygons = {}

2 for (每一个包含场景图元的物体object O)

3 GeometryPolygons = GeometryPolygons U O.PolygonSet

4 GENERATE-BSP-TREE (Tree.RootNode, GeometryPolygons)

l 分配叶节点上的取样点。

5 DISTRIBUTE-SAMPLE-POINTS (Tree.RootNode, {})

6 TRACE-VISIBILITY (Tree)

7 for 每一个场景中的静态物体object O

8 for 物体O中每一个多边形P

9 PUSH-POLYGON (Node, P)

l 函数CREATE-PATCHES是一个未定义的函数，由于我们的解决方案效率并不是太好，因此没有对它进行详细的介绍。

10 CREATE-PATCHES (Tree)

11 RADIOSITY (Tree)

复杂度分析

RENDER-SCENE中调用的函数复杂度如下：

函数	最坏情况	一般情况	描述
GENERATE-BSP-TREE	O(n2 lg n)	O(n2)	n是场景中几何体的多边形数
DISTRIBUTE-SAMPLE-POINTS	Q (np + xy)	Q (np + xy)	n是树中的多边形数，p是树中采样点数，x和y是相关节点盒包围的分割平面宽度
TRACE-VISIBILITY	O(n2)	O(n lg n)	n是树中多边形数
RADIOSITY	O(n3)	O(n2 lg n)	n是树中patch数

一般情况这列显示了算法通常运行时间的估计，但如之前提到的，从一个场景到另一个场景会有很大差异。显然主导函数是RADIOSITY，它在最坏情况导致渲染场景趋于O(n3)指数级。

第六章 BSP树中的物理学

待续。。。

终于将HL2的vbsp，vvis看完了，随便也翻了翻q3map代码，发现两者的代码太相似了，可以看出在BSP分割，portal的查找方面在Q2中都应该已经定型了，因此两者使用的算法都是一样的。下面我主要谈一下计算pvs的算法，因为在我翻译的那篇文章《bsp技术详解》中计算pvs是通过在每个portal上确定一些采样点然后进行ray cast来计算pvs的，这种方法的速度没有保证，而且处理起来也非常麻烦。而ID通过对每一个portal的polygen进行clip的方法来获取pvs，确实速度上要比上一个方法好上

很多。下面我来对算法进行详细的介绍，如果你对bsp不是很熟的话需要明确一下几个概念，一个是cluster，对于室内场景来说它完全是由cluster组成的，简单的你可以将它认为是场景中的一个房间，另一个是portal，场景中的cluster是由portal连接为一个整体，你可以把它看作是房间的门或窗户。在进行pvs计算的时候已经将整个场景划分为bsp tree，查找完portal并将cluster和leaf node连接起来了。

 

1、首先对所有的portal先进行一下预处理，让一个portal只和一个cluster发生联系，这样作的目的是为了获得一个单向的portal，也就是说portal只在一边可见，这样做是为了方便进行处理。我们知道一个portal通常连接了两个cluster，一般情况下使用的是portal所在plane正面的portal，但为了达到上述目的，我们需要将portal分为正反两个，由于在bsp中每一个plane都保存正反两个，因此位于反面的portal只需要对ploygen颠倒一下

顶点顺序即可。这里规定一个portal只和位于其plane的法线方向上的luster发生联系，预处理后保存的portal数量是原来的2倍。

2、接着我们需要对portal进行一下分类处理。通过简单的常识我们知道，由于现在每一个portal都是单向可见，因此只有位于portal可见方向（称为front方向）的portal才可能是可见的，我们需要对每一个portal都获得一个front portal列表并保存起来。

3、下面我们需要进一步的对每一个portal的front portal列表中不可见的portal进行剔除。我们知道场景完全是由一个个portal连接起来的cluste组成的，对于一个portal来说位于同一个cluster的portal一定可见，而其他portal要想可见最基本的要求是它可以通过其他portal连接到这个cluster上，因此通过portal的连接关系我们可以从front portal列表中剔除那些和当前portal没有连接关系的portal，并保存到floodportal列表中。

4、好了经过上面的处理我们已经剔除了大部分不可见的portal，可见的portal一定包含在flood portal列表中，因此需要使用更精确的方法进行检查。为了方便描述，我假定当前计算pvs的portal为A，任选和A所在的cluster ca相连的一个portal称为B，注意B一定是可见，因此B所在的cluster cb一定可见，但是和cb相连的其它portal并不一定可见，为了检查是否可见，我们假定选取其中的一个portal称为C。好了现在的问题简化为已知A和B求C是否可见，算法如下：

在A上选取一条边和B上的一个顶点构成一个clip plane，为了保证这是一个合法的clip plane我们需要做一下检查，为了简单化我们首先需要保证clip plane的法线方向必须指向portal A的外部，也就是说A上所有的顶点都位于clip plane的背面。

其次我们要保证portal B上所有的顶点都位于clip plane的正面，这样做可以保证当你选择A上最左边的一条边时必须要和B上最右边的一个顶点构成clip plane，当你选择A上最右边的一条边时必须要和B上最左边的一个顶点构成clip plane，将所有的clip plane合并起来实际上就获得一个A到B的最大可见frustum，只有位于frustum内部的portal才是可见的。当建立起这个frustum后我们就可以使用它对C的polygen进行clip操作了，当C clip后如果没有polygen在frustum内部那么它是不可见的，否则portal C可见并将可见的polygen保存下来。当C可见后我们需要接着对和C相连的portal进行检查，方法还是一样不过上面的portal B变成了C而且必须要注意，建立frustum使用C的polygen应该是clip后的polygen数据。通过上面的方法对A的flood portal列表进行递归运算最终将获得一个真正的可见portal集合保存到vis portal列表中。还需要指出一点的是建立clip plane的过程实际上需要两次，第一次是从A到B，第二次是从B到A，这样做的原因是并不是所有的极值点都位于B上的，也可能位于A上因此需要进行两次。

Q:怎么根据AB生成Frustum?

A:如果portal A和B都是一个四边形的话，frustum的四个面是这样组成的，A的左边和B的右边构成一个plane，A的右边和B的左边构成一个plane，上下方向也是，这样就形成一个frustum。但是当portal由多个顶点构成时，组成frustum的面也不会只有四个，这样形成的会是一个多面的frustum。